Products
Pricing & Plans

64-bit ARM Optimization for Audio Signal Processing

Gabor Szanto

The ARM64 platform has a bright future and it is probably one of the most important technological advances in the semiconductor field. Here at Superpowered HQ, we often are asked how we optimize the Superpowered Audio Engine for the ARM processor architecture. As we’ve just released Superpowered Audio for ARM64, we thought that we’d share a sneak peek and a few details about how we went about developing and optimizing our latest audio library.

Instead of writing a hype-y, superficial article about ARM64 (e.g. the type of articles written when the Apple A7 came out), I’d like to focus on significantly deeper (and more interesting) subjects. I’m going to give you a glimpse of how we optimize here at Superpowered. The article will flow from the non-technical to the hardcore technical, and I’m sure some of you will get lost reading this blog post.  Even so, I assure you: if ARM or DSP is interests you, you’ll learn something here.

Android and iOS Superpowered apps are faster than ever with ARM64

To be honest, we hate it when somebody says "We are porting ABC to XYZ". When used this way, "porting" only means writing a number of wrappers and hacks to make some code run on a system for which it wasn’t optimized.

If that is what ‘porting’ means to you, then we must stress that we did not “port” the Superpowered Audio SDK from 32-bit ARM to 64-bit ARM.

Instead, we completely re-wrote and re-optimized our entire codebase, using our patent-pending optimization method-the very core of Superpowered technology. As a result, we have optimized everything completely anew, from the underlying math to the last line of ARM assembly. The results we attained are:

64-bit ARM Registers and Functions

Let’s start with an easy-to-understand feature that we here at Superpowered happen to like very much and that happens to be one of the principal reasons for the improved performance of ARM64: the method in which ARM64 passes variables.

All software consists of functions, and your processor calls thousands of them every second. Heck, one of your processor’s main job is to call functions. (Yes, object-oriented programs are compiled as functions too.)

Most functions need parameters to process. 32-bit ARM can pass 4 parameters at a time to the registers. If your function needs more parameters, they have to travel via memory, in the thread’s stack. As you know, memory (even cached memory) is slower than registers. A typical call to a function on 32-bit ARM looks like this:

  1. Save the content of some of the registers to memory (preserved registers).
  2. Read additional parameters from the stack.
  3. Do stuff.
  4. Restore preserved registers from memory.
  5. Return.

As you can imagine, in this case, the stack pointer crazily goes around in cycles all the time.

64-bit ARM, on the other hand, has 8 registers for passing parameters, plus 8 additional registers for floating-point parameters. That’s enough for most functions to operate with, so a typical function call on 64-bit ARM looks like:

  1. Do stuff.
  2. Return.

ARM64 has twice the number of registers to work with. While it still has a register range to preserve between function calls, you usually don’t need to use those registers. Hence, no need to save them either!

This is one reason why ARM64 performs better than 64-bit Intel processors, and why Apple refers to ARM64 as desktop-class architecture.

ARMv8 vs ARMv7

64-bit ARM’s official name is ARMv8. The 32-bit ARM version found in most mobile devices is ARMv7 + NEON (called armeabi-v7a in Android). ARMv8 is not an extension to ARMv7 and is not an enhanced version of ARMv7; instead, it is a completely new language and processor built upon ARM’s experience with ARMv7 + NEON.

ARMv8 doesn’t have the optional NEON SIMD extension anymore, as NEON SIMD is now entirely integrated into the instruction set and the ARM processor architecture. All the previous instructions are now found in that set, but sometimes under very different names. We especially like the following new instructions:

There are a few minor setbacks. Most of the “regular” instructions are there, but the amazing conditional execution that was pioneered by ARM is unfortunately gone (although there are some conditional select instructions, and they are sufficient for our needs).

SIMD Register Packing and Permutations in ARMv8

A bigger problem was the different packing/handling of the SIMD registers. In ARMv7 there are 16x128-bit registers (Q0 to Q15), also visible as 32x64-bit registers (D0 to D31) or 64x32-bit registers. You can also separately access the first half of the 32-bit registers (S0 to S31).

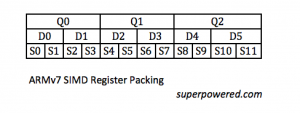
ARMv7 32bit SIMD Register Packing

This flexibility comes handy in many situations, but ARMv8 packs them differently. ARMv8 has a breathtaking number of 128-bit registers: 32! That’s 512 bytes of data directly available to process! So we have V0 to V31 (in ARMv8 they are called “V”, not “Q”).

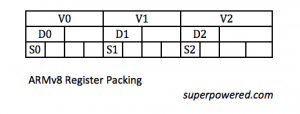
ARMv8 64bit Register Packing

Yet… we no longer have D0 to D63. Now, we only have D0 to D31 and S0 to S31, and they are no longer contiguous, occupying the lower part of the corresponding “V”.

This means we can’t only process half of the V registers, and we can’t “combine” them in-place. There are “half” instructions operating on the lower half, but they automatically zero the upper part of the V, erasing data. You can probably guess that using “half” instructions all the time removes the advantage of increased number of registers.

Furthermore, permutation instructions (reordering data, such as zip, unzip or transpose) work differently. They were in-place in ARMv7, but now they must have a target.

This means that you can’t perform these operations in-place anymore. Instead, you now require at least an extra register to do the job. It turns out that this is not a limitation as having a different target can be useful, but it’s very different than what we were used to in in ARMv7.

Due the changes detailed above (and others that we didn’t mention), ARMv7 NEON code/algorithms cannot be simply "translated" to ARMv8. We had to rethink everything from scratch, often resulting in an entirely different solution.

Interesting Observations when optimizing for 64-bit ARM

The special DCT-32 (discrete cosine transform) function in MP3 decoding was an edge case. Not even a single component of our previous ARMv7 solution would work this time, so we had to restart and rewrite the entirety from scratch.

Our result was 20% faster (on 32-bit ARM too!), but we spent a lot more time with its implementation than we had originally estimated.

It’s easy to assume that twice the amount of registers would theoretically mean an automatic 2x increase in processing speed, amirite?

Nope!

It is worth noting that many algorithms don’t actually benefit that much from extra registers, as they may have dependencies on earlier samples (like filters) or because the memory bus is a bottleneck for the best, most efficient DSP implementations.

A great exception to this observation, however, was the SuperpoweredBandpassFilterbank, wherein we process multiple filters on the same audio data. In this special case, we could fully utilize the increased register space. Executing twice as many filters at the same time resulted in twice the speed, which was great for us to see.

Fused!

Our FFT solution became faster, and more precise than Apple’s vDSP, thanks to the fused multiply-add instructions in ARMv8. Multiply-add is:

x = a + b * c

Previously, the processor handled it as two separate instructions: one multiplication plus one addition. As floating-point operations may have rounding errors, two rounding errors were added together in ARMv7.

But ARMv8’s multiply-add is “fused”, it’s not handled as two separate instructions, so you get just one rounding error. Interestingly, Apple’s vDSP on 64-bit ARM does not take the advantage of the fused multiply-add instruction, so it’s less precise.

Implementing the fastest cube root for MP3 and AAC decoding

Thank you reading so far, you are amazing! Now, let us show you a glimpse of how we optimized a common part of MP3 and AAC decoders: the dequantizer.

After Huffman decoding, all data should be raised to the power of 4/3, so we need to calculate:

x4/3

You can find a general, parallelizable implementation here.

However, general solutions aren't useful to us, since we at Superpowered are always seeking the highest performance with which to imbue our creator-customers with super powers!

Not counting the loads and moves, that solution needs 23 instructions and 18 coefficients (taking 4.5 Q/V registers). As we have a fixed power (4/3), there must be a more efficient way. What’s the equation here?

x4/3 = x * ∛x

Aha!

So we need to find a very fast cube root solution instead, and the Internet has a lot more ideas on how to attack that problem.

Nota bene: We are not optimizing for the best mathematical accuracy attainable on the 32-bit processor. We are optimizing for a certain level of accuracy where the result of the MP3/AAC audio output is equal to the result achieved if we had used the most accurate function.

Remember the famous fast inverse square root bit hack in Quake III? It’s attributed to John Carmack, but it’s probably based on the roots of early computer graphics (eg Silicon Graphics or 3dfx Interactive). They figured out a method where the solution is basically cut into two parts:

  1. Make a very good guess with evil bit level float hacking.
  2. Iterate over the result to make it more precise.

The great Hacker’s Delight book has a few fast cube root solutions based along these lines, with various precisions.

The Good Guess

We pick the most precise initial guess achievable with bit level float hacking (treat the floating point input X as an integer I):

I = I / 3 + 0x2a51067f

The constant 0x2a51067f balances the relative error and it’s based on the logarithmic structure of the IEEE 32-bit floating number.

(BTW this could be an entire article on it’s own, but here is a link if you’re interested.)

There is another bit hack here: integer division by 3. No such instruction exists, but it’s a well-known hack performed like this:

I / 3 = (I * 0x55555556) >> 32

So the end result for our good guess is:

x4/3 ~ ((I * 0x55555556) >> 32) + 0x2a51067f

This result needs only three instructions: long multiply, permutation (in order to take the upper halves from multiple registers) and addition. Precision is at 0.0316, which is "good enough for government work", but not good enough for Superpowered since it would result in ~1% audio distortion for MP3 and AAC.

We need a second step to make it more precise.

The Second Step

We iterate over the result to make it more precise. Several mathematical methods exist for this, and some of them are surprisingly old. Newton (the guy with the apple) and Halley (the guy with the comet) both invented good solutions that are still in use today. The processors in your computing devices make use of them all the time in solving trigonometric functions; they’re probably doing it right now as you read this sentence.

All of these methods include division, which is still expensive in terms of CPU cycles despite ARMv8’s native FDIV instruction. The Hacker’s Delight book’s high precision functions are based on Newton’s steps, but they are quite expensive in our case, as our desired accuracy required running them twice.

We tested all sorts of methods to discover performant results, and finally we discovered a solution that needs only one step.

The Superpowered Solution

Our dequantizer consists of 18 instructions, and just one of them is a division. Instead of having 18 coefficients, we only have two magic numbers, thus taking 1.25 Q/V register. The speed is 19x faster vs the un-optimized C implementation.

We hope you enjoyed this sneak-peek into how we think when we want to optimize audio signal processing quality, power consumption and efficiency, and of course, speed in order to superpower creators like you!

  • 64-bit ARM
  • Android ARM
  • ARM registers
  • ARM68
  • ARMv7